kdb+ »

kdb standard SQL support s)

February 24th, 2016 by admin

First, in case you haven’t heard about it kdb has a standard SQL mode, you can send queries prefixed with s) and they will be interpreted as standard SQL like so:

t:([] a:til 10; b:10?9.0; c:10#`a`b`c)

q)select * from t where a>5 and b<5
'rank
q)s)select * from t where a>5 and b<5
a b        c
------------
6 4.765327 a
8 2.066954 c


q)select from t where a>5,b<5
a b        c
------------
6 4.765327 a
8 2.066954 c

Notice how the standard “and” syntax worked when I used s) but without it, q’s right to left evaluation causes problems. It’s about now that a lot of people get very excited, they think great I can skip learning that q-sql and use my standard SQL. Sometimes the look of joy on their faces transforms to frustration once they start using it. So let’s look at what works:

Operation	Works?
Standard SQL Inserts	Yes
ORDER BY	half works
COUNT	Yes
DELETE	Yes
UPDATE	Yes
String matching	slightly works
NOT	NO
IN	Yes
GROUP BY	Yes
LIMIT / TOP	NO
Date Times	NO

Standard SQL Inserts work

q)s)insert into t (a, b, c) values (6, 9.0, 'symboll');
q)s)insert into t (a, b) values (6, 9.0);
q)t
a b         c
-------------------
0 4.438651  a
1 5.206683  b
2 0.7549972 c
3 1.763917  a
4 3.380742  b
5 5.523707  c
6 4.765327  a
7 6.224489  b
8 2.066954  c
9 6.227578  a
6 9         a
6 9         symboll
6 9

ORDER BY half works

“ORDER BY” will sort the columns in ascending order, attempting to use DESC has no effect.

q)s)SELECT * FROM t ORDER BY b DESC;
a b         c
-------------------
2 0.7549972 c
3 1.763917  a
8 2.066954  c
4 3.380742  b
0 4.438651  a
6 4.765327  a
1 5.206683  b
5 5.523707  c
7 6.224489  b
9 6.227578  a
6 9         a
6 9         symboll
6 9

q)s)SELECT * FROM t ORDER BY b ASC;
a b         c
-------------------
2 0.7549972 c
3 1.763917  a
8 2.066954  c
4 3.380742  b
0 4.438651  a
6 4.765327  a
1 5.206683  b
5 5.523707  c
7 6.224489  b
9 6.227578  a
6 9         a
6 9         symboll
6 9

COUNT works

q)s)SELECT count(*) FROM t
i
--
13

DELETE works

q)s)DELETE FROM t WHERE a>=6
q)t
a b         c
-------------
0 4.438651  a
1 5.206683  b
2 0.7549972 c
3 1.763917  a
4 3.380742  b
5 5.523707  c

UPDATE works

q)s)UPDATE t SET a=999 WHERE b>5;
q)t
a   b         c
---------------
0   4.438651  a
999 5.206683  b
2   0.7549972 c
3   1.763917  a
4   3.380742  b
999 5.523707  c

String matching slightly works

q)s)SELECT * FROM t where c='a'
a b        c
------------
0 4.438651 a
3 1.763917 a

q)s)SELECT * FROM t where c like '%a%'
a b        c
------------
0 4.438651 a
3 1.763917 a

// This is valid for SQL server etc.
q)s)SELECT * FROM t where c like '_'
a   b         c
---------------
0   4.438651  a
999 5.206683  b
2   0.7549972 c
3   1.763917  a
4   3.380742  b
999 5.523707  c

// This should not return results in standard SQL
q)s)SELECT * FROM t where c like '?'
a   b         c
---------------
0   4.438651  a
999 5.206683  b
2   0.7549972 c
3   1.763917  a
4   3.380742  b
999 5.523707  c

NOT fails

q)s)SELECT * FROM t where c NOT LIKE '%a%'
'type

Modifying our String query slightly by adding NOT throws an error. My guess is that the interpreter has got confused.

IN works

q)s)SELECT * FROM t where c in ('a','b');
a   b        c
--------------
0   4.438651 a
999 5.206683 b
3   1.763917 a
4   3.380742 b
q)s)SELECT * FROM t where a in (0,3);
a b        c
------------
0 4.438651 a
3 1.763917 a

GROUP BY works

q)s)SELECT a,min(b) FROM t GROUP BY a
a   b
-------------
0   4.438651
2   0.7549972
3   1.763917
4   3.380742
999 5.206683

LIMIT / TOP does not work

q)s)select TOP 2 * FROM t;
'from
q)s)select * FROM t LIMIT 2;
a   b         c
---------------
0   4.438651  a
999 5.206683  b
2   0.7549972 c
3   1.763917  a
4   3.380742  b
999 5.523707  c

Date Times Don’t Work Right

q)a:.z.p + 1000000000*til 10
q)s:([] p:a; t:`time$a; n:`timespan$a; d:`date$a)
q)s
p                             t            n                    d
--------------------------------------------------------------------------
2016.02.24D14:27:53.095171000 14:27:53.095 0D14:27:53.095171000 2016.02.24
2016.02.24D14:27:54.095171000 14:27:54.095 0D14:27:54.095171000 2016.02.24
2016.02.24D14:27:55.095171000 14:27:55.095 0D14:27:55.095171000 2016.02.24
2016.02.24D14:27:56.095171000 14:27:56.095 0D14:27:56.095171000 2016.02.24
2016.02.24D14:27:57.095171000 14:27:57.095 0D14:27:57.095171000 2016.02.24
2016.02.24D14:27:58.095171000 14:27:58.095 0D14:27:58.095171000 2016.02.24
2016.02.24D14:27:59.095171000 14:27:59.095 0D14:27:59.095171000 2016.02.24
2016.02.24D14:28:00.095171000 14:28:00.095 0D14:28:00.095171000 2016.02.24
2016.02.24D14:28:01.095171000 14:28:01.095 0D14:28:01.095171000 2016.02.24
2016.02.24D14:28:02.095171000 14:28:02.095 0D14:28:02.095171000 2016.02.24

q)s)SELECT *  FROM  s WHERE d > '2016-02-23'
'type
// The below does work:
// q)s)SELECT *  FROM  s WHERE d > 2016.02.23

Overall standard SQL support in kdb has got much better. However I would still recommend only using the s) syntax for plugging into an existing jdbc/odbc visualization tool and getting some immediate simple results. For any form of complex queries on strings, joins etc. support is either not there or the result may not be what you expect.

kdb+ 3 Comments

qStudio kdb IDE 1.40 Released

February 15th, 2016 by admin

qStudio 1.40 is now available to download.

The latest changes include:

No need to save changes before shutdown, unsaved changes stored till reopened.
Add sqlchart to system path.
Fix display of tables with underscore in the name.
Database documenter/report enhancements
Improved code printing
FileTreePanel much more efficient at displaying large number of files.

kdb+,qStudio Add a comment

KX closes down commercial 32 bit kdb, open alternatives?

November 5th, 2015 by John Dempster

Previously on our blog we had a lively debate about a possibly Open Sourced kdb+ , unfortunately kx now seems to be moving the opposite direction. In a recent announcement they are now restricting “32-bit kdb+ for non-commercial use only”. The timing is particularly unfortunate as:

More column oriented databases are becoming available.
One of those databases: Greenplum just announced that it is going open source

Alternative (far less enterprise proven) solutions are available:

MAN AHL have released Arctic an open source Market Data platform based on python and MongoDB
Kerf Database – A DB aimed at the same market as kdb has now partnered with Briarcliff-Hall and is making greater sales inroads

This renewed interest in kdb alternatives hasn’t so far delivered a kdb+ killer but I fear in time it will.

kdb+,timeseries 3 Comments

kdb code highlighting in intellij

May 2nd, 2015 by admin

An intellij keyword file is now available to provide syntax highlighting of kdb code in intellij:

q Code Intellij Highlighting

To install it copy this xml file to this directory:
C:\Users\USERNAME\.IdeaIC14\config\filetypes
Where USERNAME is obviously your username. Then restart intellij and open a .q file.

We’ve updated our notepad++ qlang.xml to provide code folding and highlighting of the .Q/.z namespaces.

kdb+ Add a comment

kdb qunit testing now open source on github

May 2nd, 2015 by admin

We’ve now posted all source code from this website on our github kdb page.

Additionally we are open sourcing qunit, our kdb testing framework.
We look forward to receiving pull requests to fix our (hopefully few) bugs.

kdb+ Add a comment

qStudio adds Nested Server Folder Support

April 23rd, 2015 by admin

Since our last qStudio kdb+ IDE announcment we have added a lot of new features:

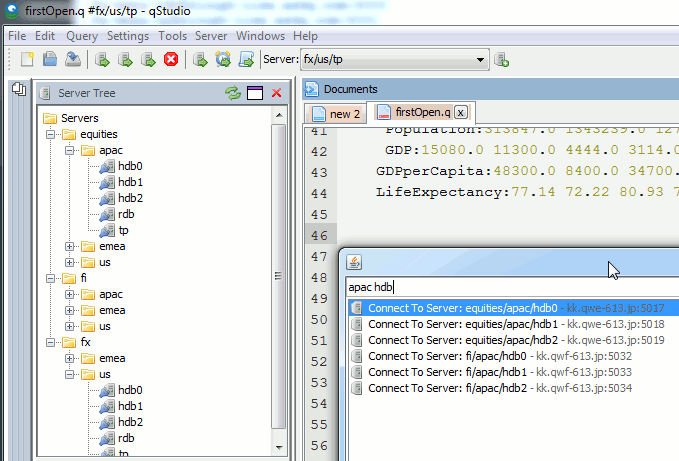
Bulk importing kdb server lists

There’s a lot of new features to allow supporting a huge number of servers efficiently:

Support importing HUGE number of servers:
- 5000+ server connections are now supported
- To prevent massive memory use, the object tree for a server is no longer refreshed at startup only on connection.
- Allow specifying default username/password once for all servers
- Allow nested connection folders
- Add critical color option – servers with prod in name get highlighted in red
Sort File Tree Alphabetically
Numerous bugfixes including:
- Fix critical Mac bug that prevented launching in some instances
- Fix query cancelling

kdb+,qStudio Add a comment

Open Sourced kdb+

January 19th, 2015 by Ryan Hamilton

In a world overran with open source big data solutions is kdb+ going to be left behind? I hope not…

Every few weeks someone comes to me with a big data problem often with a half-done mongoDB/NoSQL solution that they “want a little help with”. Usually after looking at it I think to myself

“I could solve this in 20 minutes with 5 lines of q code”

But how do I tell someone they should use a system which may end up costing them £1,000s per core in licensing costs. Yes it’s great that there’s a free 32-bit trial version but the risk that you may end up needing the 64-bit is too great a risk.

kdb+ vs mongoDB database popularity

Given the ever-increasing number of NoSQL solutions and in particular the rising popularity of Hadoop, R, python and MongoDB it’s not hard to see that open-source is taking over the world. Right now kdb+ still has the edge, that it’s faster, sleeker, sexier..but I don’t think that will save it in the long run. The power of open-source is that it let’s everyone contribute, witness the 100’s of libraries available for R, the 1000’s of javascript frameworks. The truly sad thing is that it’s not always the best underlying technology that wins. A 1000 amateurs creating a vibrant ecosystem of plug-ins, add-ons, tutorials… can beat other technologies through sheer force of numbers.

APL was a great language yet it remains relegated to history while PHP flourishes.
PostgreSQL was technically superior to MySQL yet MySQL is deployed everywhere

I believe kdb+ is the best solution to a large number of “big data” problems (small data to kdb+), When you stop and think, time-series data is everywhere, open sourcing kdb+ would open up entirely new sectors to kdb+ and I hope it’s a step kx take before it’s too late.

What do you think? Leave your comments below.

kdb+,timeseries 10 Comments

qStudio kdb+ GUI adds Dark Theme and Chinese Language

October 20th, 2014 by admin

Based on user requests we have released a number of new features with qStudio 1.36:

Download the latest ->qStudio<- now.

Dark Code Editor Themes

Which can be set under settings->preferences

qstudio-settings-preferences

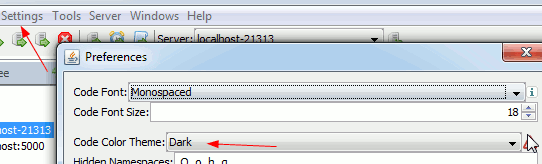
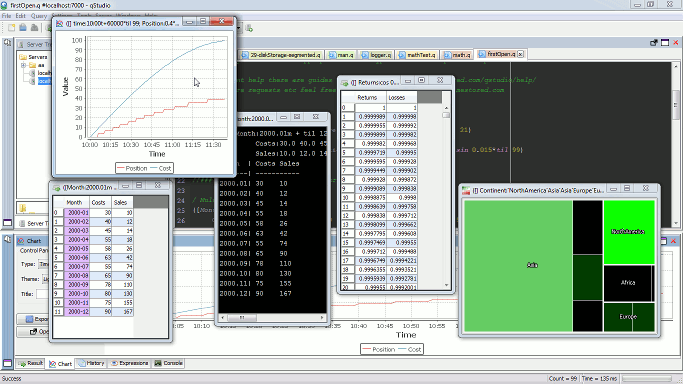
Open Results and Charts in New Window

To expand a panel into a new window click the “pop-out” icon.
pop-out

This will bring up the result in a new window:

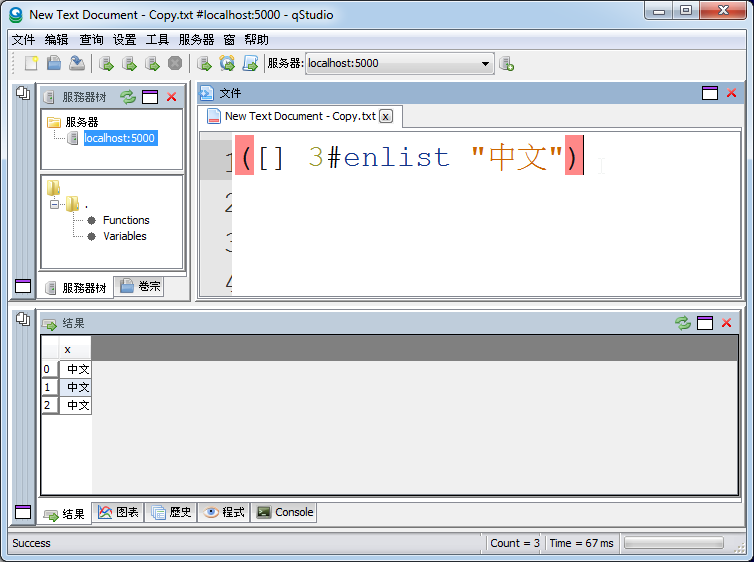
UTF-8 Chinese Language Support

qstudio-utf8

Tags: kdb+, qstudio. kdb+,qStudio Add a comment

Developer Salary by Location

October 8th, 2014 by admin

kdb+ London Contract – £800 p/day
kdb+ belfast Citigroup Contract £400 p/day
Java Poland £150 p/day

kdb+ Add a comment

Command Line Kdb+ Charts

September 8th, 2014 by admin

sqlDashboards are included as a bundle with qStudio, part of that package is a command line utility called sqlChart that allows generating customized sql charts from the command line.

Checkout the video to see how you can create a chart based on data from a kdb+ database in 2 minutes:

The sqlChart page has all the documentation you need, Download the qstudio.zip to try it now.

The q Code

C:\temp\ch\qstudio>sqlchart -s kdb -P 5000 -e "([] dt:2013.01.01+til 21; cosineWave:cos a; sineWave:sin a:0.6*til 21)" -c timeseries -W 600 -t  dark
C:\temp\ch\qstudio\out.png

Help Screen

C:\temp\ch\qstudio>sqlchart
Option (* = required)             Description
---------------------             -----------
-?, --help                        Display a help message and exit.
-D, --database <db_name>          The database to use.
-H, --height <output_height>      Set the height of the chart output
                                    (default: 300)
-P, --port <port_num>             The TCP/IP port number to use for the
                                    SQL Server connection.
-W, --width <output_width>        Set the width of the chart output
                                    (default: 400)
-c, --chart <chart_type>          Set the selected chart type. Options
                                    available: timeseries, areachart,
                                    barchart, bubblechart, candlestick,
                                    datatable, heatmap, histogram,
                                    linechart, noredraw, piechart,
                                    scatterplot (default: barchart)
-e, --execute <sql_statement>     Execute the selected sql statement.
-h, --host <host_name>            SQL server host that will be queried.
                                    (default: localhost)
-o, --out <file_name>             The name of the destination image
                                    file. (default: out.png)
-p, --password <password>         Password used to connect to SQL server.
* -s, --servertype <server_type>  The type of sql server being queried.
                                    Valid values include:kdb,mysql,
                                    postgres,mssql,h2.
-t, --theme <color_theme>         Set the color theme for the chart.
                                    Options available: light,dark,pastel
                                    (default: light)
-u, --user <user_name>            Username used to connect to SQL server.

Tags: kdb chart, kdb+, qstudio, timeseries. kdb+,qStudio Add a comment

TimeStored Blog

Archive for the 'kdb+' Category

kdb standard SQL support s)

Standard SQL Inserts work

ORDER BY half works

COUNT works

DELETE works

UPDATE works

String matching slightly works

NOT fails

IN works

GROUP BY works

LIMIT / TOP does not work

Date Times Don’t Work Right

qStudio kdb IDE 1.40 Released

KX closes down commercial 32 bit kdb, open alternatives?

kdb code highlighting in intellij

kdb qunit testing now open source on github

qStudio adds Nested Server Folder Support

Open Sourced kdb+

qStudio kdb+ GUI adds Dark Theme and Chinese Language

Dark Code Editor Themes

Open Results and Charts in New Window

UTF-8 Chinese Language Support

Developer Salary by Location

Command Line Kdb+ Charts

The q Code

Help Screen